Единична векторна нотация | Вектори и пространства | Линейна алгебра | Академия Хан
Когато обясняват измерение W, то се представя като отрицателната страна на оста X. Защо Dimension W е отрицателен X? Наистина ли не е собствено измерение?

- Опитайте да нарисувате 4-измерна графика на 2-измерна повърхност. Това е, което те измислиха (вашето право, макар че не е страхотна графика).
Както @NendoTaka спомена, е доста трудно да се направи 4d обект на 2d повърхност.
Ето как работи размерността:
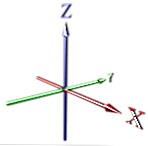
с едно измерение, точка се изпраща безкрайно, създавайки линия (виж X)
в 2d, добавяме размер, перпендикулярен на това (виж X, Y).
След това отново отиваме перпендикулярно и се разширяваме нагоре, за да получим третото измерение (Вижте X, Y, Z).
Тъй като 3d> 2d, не можем да представим толкова добре на хартия, без да сгъваме хартията или да добавяме повече листове отгоре й - всичко това е наистина непрактично за гледане на екран. Затова вместо това използваме перспектива - как очите ни възприемат 3d. Обикновено ъглите тук са ~ 30 градуса.

И това изглежда доста добре, защото очите ни не виждат в този традиционен 3D смисъл, така че имитира това работи. Но когато искаме да представим 4-то измерение, нямаме с какво да го сравним. Трябва отново да отидем перпендикулярно и това е трудно за нашите очи да разберем, тъй като нямаме много референция.
Ето примерно изображение на 4-то измерение:
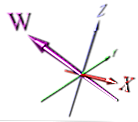
Това е по-правилен начин за показване на измерението, но все пак разчита на перспектива - също така не е веднага очевидно, че това е ново измерение на пръв поглед.
Аниматорите вероятно са избрали да направят нещо просто, което би било по-лесно да се анимира. Въпреки че, ако завъртите горното изображение, размерите X и W могат да се припокрият - и това не би било очевидно в изображението без указатели на стрелки.
Така че, да, грешат - но също така не е лесен начин да представите 4 измерения на един лист хартия
Координиране на източници на изображения и добро четене
3- 1 За да бъдем честни, има много стандартни начини за проектиране на 4-измерни обекти като тесеракти и 3-сфери в 3 измерения (и след това до 2 измерения по обичайните начини), които са значително по-добри от използвания в шоуто, много от които имат допълнителен бонус да изглеждат по-хладни от този, използван в шоуто.
- @senshin о, със сигурност, но предполагам, че аниматорите също са искали да обяснят нещо, вместо да изумяват
- 1 Можете да използвате други неща освен позицията, за да посочите колко далеч по дадена ос е нещо, като цвят.







